🌱

Dec 15, 20243 min read

Properties of Context Free Languages and Turing Machines

Context-Free Grammar (CFG): S -> aS | b

A context-free grammar (CFG) is a formal way to describe the syntax of languages. It consists of:

  1. A set of production rules, like S -> aS | b, which dictate how strings in the language are formed.
  2. Terminals: The actual characters in the language (e.g., a, b).
  3. Non-terminals: Variables (e.g., S) that are placeholders for patterns in the language.
  4. Start symbol: The initial non-terminal that generates strings.

For example, in the rule S -> aS | b, we have:

  • S: A non-terminal that can generate more characters.
  • a and b: Terminals (characters from the language).
  • |: Means “or”, so S can either become aS or b.

Types of CFG

A CFG can be:

  • linear: S->aSb|L one non terminal on RHS
  • non-linear: S->aSb|bSa|SS|L more than one non terminal on RHS

Example Rule: S -> aS | b

This rule generates strings that consist of one or more as followed by a single b. Here’s how it works:

  1. Start with S:
S
  1. Apply the rule S -> aS:
aS
  1. Apply the rule again S -> aS:
aaS
  1. Keep applying until you want to stop with S -> b:
aaab

Thus, the string aaab is generated by applying the production rules step-by-step.

Derivations

A sequence of applications of production rules. For the above rule, here’s an example:

  1. Start with S.
  2. Apply S -> aS:
S -> aS
  1. Apply S -> aS again:
aS -> aaS
  1. Finally, apply S -> b:
aaS -> aaab

So, the derivation for aaab is:

S -> aS -> aaS -> aaab

Example Strings

Using the rule S -> aS | b, the following strings can be generated:

  • b (by directly applying S -> b)
  • ab (by applying S -> aS, then S -> b)
  • aab (by applying S -> aS -> aS -> b)
  • aaab, aaaab, and so on (more as followed by one b).
  • Recursion: The rule S -> aS is recursive because S can call itself. This allows for generating strings with any number of as.
  • Termination: The recursion stops when we use the rule S -> b, ensuring that the string eventually ends with a b.

String belongs to Grammar or not?

  1. Start with the S start symbol and choose the closest production that matches to the given string.
  2. Replace the Variables with its most appropriate production. Repeat the process until the string is generated or until no other productions are left.

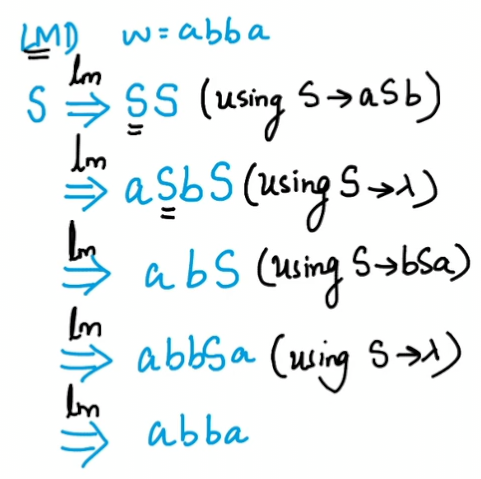
Left and Rightmost

Leftmost derivation

Rightmost Derivation

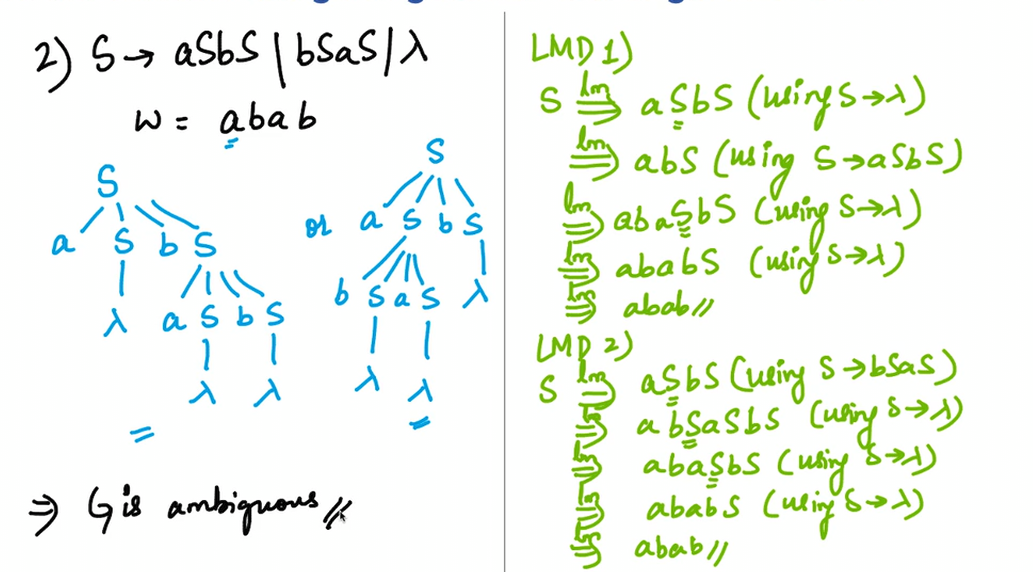
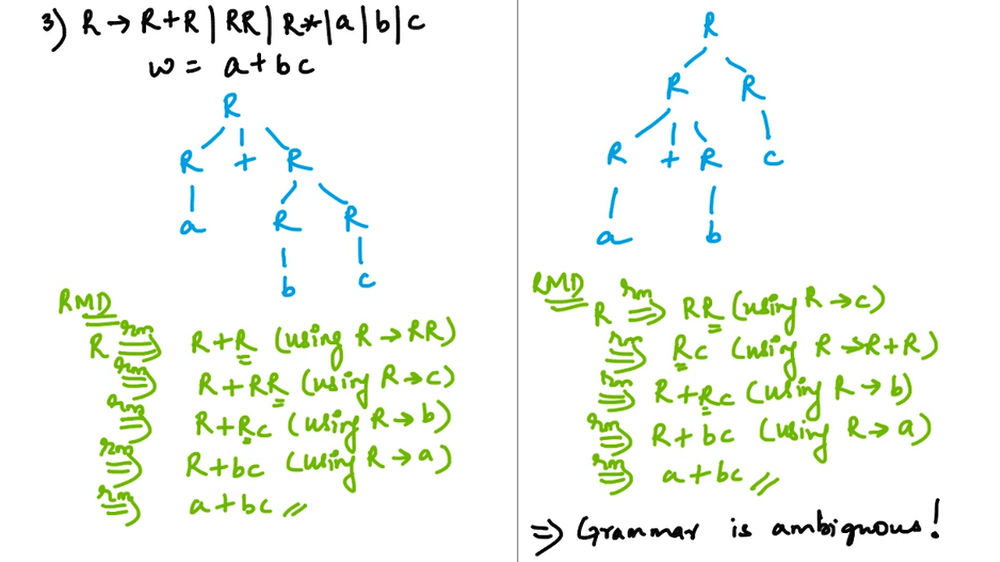
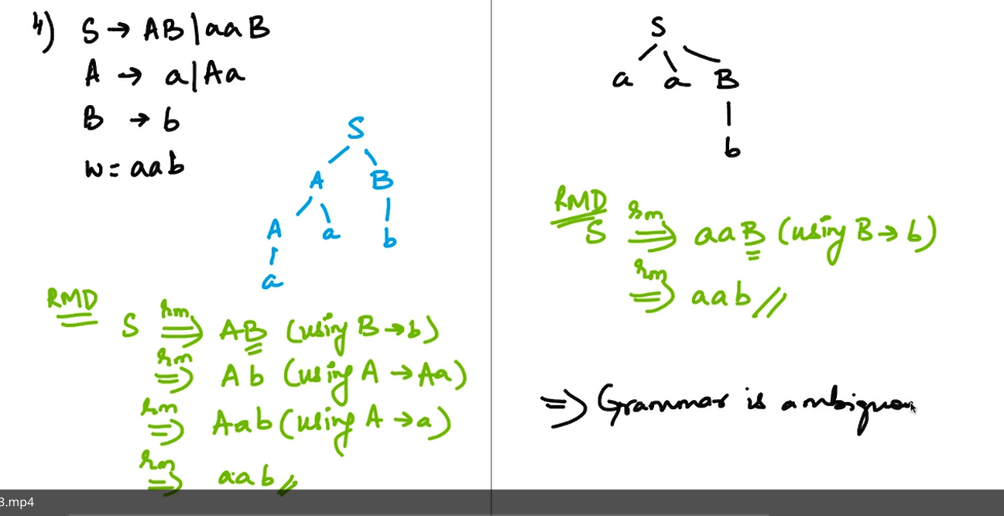
Ambiguous Grammar

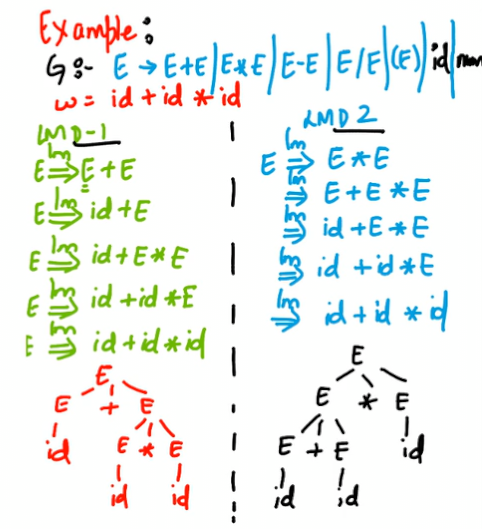
Warning

The left one is the right one! A compiler can not understand ambiguous grammar.

a+bc

Regex

aab

Grammar vs Language Ambiguity

Normal Forms

To sanitize grammar for the compiler.

  • CNF
  • GNF
  1. Membership problem: a string is a part of the language or not?
  2. Enabled parsing: you must stop after K steps, quit if over limit.

CNF

  1. Eliminate L productions
  2. Eliminate unit productions: each step must increase the length of the sentencial form or the number of terminals.
  3. Eliminate useless productions and symbols.
    1. Deriviablility: each variable must derive a string / end with set of terminals or L
    2. Reachability: each variable must be reachable from S

CNF Examples

Graph View

Backlinks